Dear Friends,
Click the link to view the images/access the links.
http://plus.maths.org/content/richard-elwes&src=fpii
Be Well.
David Exotic spheres, or why 4-dimensional space is a crazy place
by Richard Elwes
The world we live in is strictly 3-dimensional: up/down, left/right, and forwards/backwards, these are the only ways to move. For years, scientists and science fiction writers have contemplated the possibilities of higher dimensional spaces. What would a 4- or 5-dimensional universe look like? Or might it even be true, as some have suggested, that we already inhabit such a space, that our 3-dimensional home is no more than a slice through a higher dimensional realm, just as a slice through a 3-dimensional cube produces a 2-dimensional square?
Just as a 3-dimensional object can be projected onto a 2-dimensional plane, so a 4-dimensional object can be projected onto 3-dimensional space. This image comes from the projection of a 4-dimensional hypersphere. The curves are the projections of the hypersphere's parallels (red), meridians (blue) and so-called hypermeridians (green). Image by Claudio Rocchini, via Wikimedia Commons.According to the early 20th century horror writer H.P. Lovecraft, these higher dimensions do indeed exist, and are home to all manner of evil creatures. In Lovecraft's mythology, the most terrible of these beings goes by the name of Yog-Sothoth. Interestingly, on the rare occasions that Yog-Sothoth appears in the human realm, it takes the form of "a congeries of iridescent globes... stupendous in its malign suggestiveness".
Lovecraft had some interest in mathematics, and indeed used ideas such as hyperbolic geometry to lend extra strangeness to his stories (as Thomas Hull has discussed in Math Horizons). But he could not have known how fortunate was the decision to represent Yog-Sothoth in this manner. Strange spheres really are the keys to higher dimensional worlds, and our understanding of them has increased greatly in recent years. Over the last 50 years a subject called differential topology has grown up, and revealed just how alien these places are.
Higher dimensions and hyperspheres
Do higher dimensions exist? Mathematics provides a surprisingly emphatic answer to this question. Just as a 2-dimensional plane can be described by pairs of coordinates such as (5,6) with reference to a pair of axes, so 3-dimensional space can be described by triples of numbers such as (5,6,3). Of course we can continue this line of thought: 4-dimensional space, for a mathematician, is identified with the sets of quadruples of real numbers, such as (5,6,3,2). This procedure extends to all higher dimensions. Of course this does not answer the physicist's question, of whether such dimensions have any objective physical existence. But mathematically, at least, as long as you believe in numbers, you don't have much choice but to believe in 4-dimensional space too.
Well that is fine, but how can such spaces be imagined? What does the lair of Yog-Sothoth actually look like? This is a much harder question to answer, since our brains are not wired to see in more dimensions than three. But again, mathematical techniques can help, firstly by allowing us to generalise the phenomena that we do see in more familiar spaces.
An important example is the sphere. If you choose a spot on the ground, and then mark all the points which are exactly 1cm away from it, the shape that emerges is a circle, with radius 1cm. If you do the same thing, but in 3-dimensional space, we get an ordinary sphere or globe. Now comes the exciting part, because exactly the same trick works in four dimensions, and produces the first hypersphere.
What does this look like? Well, when we look at the circle from close up, each section looks like an ordinary 1-dimensional line (so the circle is also known as the 1-sphere). The difference between the circle and the line is that when viewed from afar, the whole thing curves back to connect to itself, and has only finite length. In the same way, each patch of the usual sphere (that is to say, the 2-sphere) looks like a patch of the 2-dimensional plane. Again, these patches are sewn together in a way that leaves no edges, and has only finite area. So far, so predictable, but exactly the same thing is true for the first hypersphere (or 3-sphere): each region looks just like familiar 3-dimensional space. We might be living in one now, for all we can see. But just like its lower dimensional cousins, the whole thing curves around on itself, in a way that flat 3-dimensional space does not, producing a shape with no sides, and only finite volume. Of course we do not stop here: the next hypersphere (the 4-sphere), is such that every region looks like 4-dimensional space, and so on in every dimension.
From geometry to topology to differential topology
Like geometry, topology is a branch of mathematics which studies shapes. One of the fundamental questions to ask is when two shapes are really the same. This does not have a unique answer, it depends on the aspects of the shape that you are most interested in. At a basic level, if two shapes are identical, but are situated in different places, then for most purposes we will count them as being "the same".
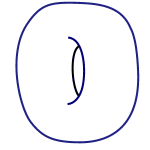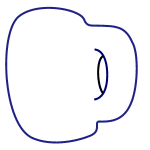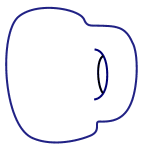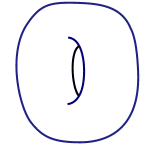In topology a doughnut and a mug are the same because one can be morphed into the other.Topology has a much broader notion of sameness than geometry. Here, two shapes are deemed "the same" if one can be pulled, stretched and twisted into the form of the other. So, to a topologist, triangles, trapeziums, septagons, and so on are all the same: they are all just circles. On the other hand, a figure of 8 is a genuinely different shape, because the topological definition of sameness never extends to cutting or gluing the shape. So an 8 can never be pulled into the shape of a circle as cutting is forbidden, and neither can a lower case i, as the two parts cannot be glued together.
If you are interested in things like angles, lengths, or areas, then the topological viewpoint is the wrong one. But a lot of important data is retained at this level: a famous example is the London tube map. Here, it is not the lengths or precise routes of the tunnels which matter, but things like the orders of the stations, and the ways that different tube lines intersect. These phenomena are topological in nature, and survive topological morphing. This is convenient, as it allows Londoners to use the famous simplified schematic map, rather than a detailed map of the whole city, incorporating the exact routes of all the tube lines.
Some shapes, such as the donut-shaped torus, have holes in them. These holes are essential; they cannot be removed by topological twisting or stretching. But which are the shapes with no holes? The most famous theorem in topology, the Poincaré conjecture, provides an elegant answer to this question: it says that the only such shapes are the spheres. This is not true from a geometrical viewpoint, as cubes, pyramids, dodecahedra, and a multidue of other shapes all have no holes. But, of course, to a topologist, all these exciting shapes are nothing more than spheres.
We have known since 2002 that the Poincaré conjecture is indeed true (find out more on Plus). Henri Poincaré's original question concerned the 3-sphere, but in fact exactly the same thing applies in all higher dimensions too. The fact is that, when viewed topologically, spheres are beautifully simple and unique objects in every dimension. However, in 1956 the first evidence arrived that a slight change in perspective would make the story hugely more complicated. When approached through the new subject of differential topology, higher dimensional spaces began to reveal some of their extraordinary secrets.
Gaps, kinks, and corners
The difference between plain topology and differential topology seems very subtle, but turns out to have astonishing consequences. It hinges on the precise type of pulling and stretching which are allowed during the morphing process. This has a dramatic impact on the shapes which are deemed to be "the same".
This is a fractal called a Julia set. Its outline is continuous, but nowhere smooth. The divide is between processes which are continuous, meaning that they do not jump or tear, and others which are smooth. Smoothness is a much stronger condition than mere continuity. The same distinction applies to shapes themselves: circles and spheres are examples of smooth shapes, while squares and cubes are not smooth because of their sharp edges and corners. All of these are continuous, however, because their edges do not have any gaps or jumps. (A discontinuous line is one which comes in two separate pieces.) There are even fractal patterns which are continuous everywhere, but not smooth anywhere.
In the same way, we can distinguish between morphing which is truly smooth, and that which is merely continuous, but potentially very jerky and violent. It is not at all obvious, however, that this distinction should really matter very much. Might it really be possible that two shapes (also called manifolds by topologists) could be the same from a topological perspective (in technical terms, be homeomorphic), but not the same from a differential perspective (they are not diffeomorphic)? In other words, can we have two shapes that can be morphed into each other without cutting, but for which the morphing can't be smooth, it requires jerks and jumps? This is certainly difficult to imagine, not least because it never happens in dimensions 1, 2, or 3.
Exotic spheres
In 1956, John Milnor was investigating 7-dimensional manifolds when he found a shape which seemed very strange. On one hand, it contained no holes, and so it seemed to be a sphere. On the other hand, the way it was curved around was not like a sphere at all. Initially Milnor thought that he had found a counterexample to the 7-dimensional version of the Poincaré conjecture: a shape with no holes, which was not a sphere. But on closer inspection, his new shape could morph into a sphere (as Poincaré insists it must be able to do), but - remarkably - it could not do so smoothly. So, although it was topologically a sphere, in differential terms it was not.
Milnor had found the first exotic sphere, and he went on to find several more in other dimensions. In each case, the result was topologically spherical, but not differentially so. Another way to say the same thing is that the exotic spheres represent ways to impose unusual notions of distance and curvature on the ordinary sphere.
In dimensions one, two, and three, there are no exotic spheres, just the usual ones. This is because the topological and differential viewpoints do not diverge in these familiar spaces. Similarly in dimensions five and six there are only the ordinary spheres, but in dimension seven, suddenly there are 28. In higher dimensions the number flickers around between 1 and arbitrarily large numbers:
| Dimension | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Number of spheres | 1 | 1 | 1 | ? | 1 | 1 | 28 | 28 | 6 | 992 | 1 | 3 | 2 | 16256 | 2 | 16 | 16 |
The realm which remains the most mysterious, even today, is 4-dimensional space. No exotic spheres have yet been found here. At the same time no-one has managed to prove that none can exist. The assertion that there are no exotic spheres in four dimensions is known as the smooth Poincaré conjecture. In case anyone has got this far and is still not sure, let me make this clear: the smooth Poincaré conjecture is not the same thing as the Poincaré conjecture! Among other differences, the Poincaré conjecture has been proved, but the smooth Poincaré conjecture remains stubbornly open today.
The weird world of four dimensions
This is the projection involving a 4-dimensional object called a dodecaplex. Image crated by Paul Nylander. So, is the smooth Poincaré conjecture true? Most mathematicians lean towards the view that it is probably false, and that 4-dimensional exotic spheres are likely to exist. The reason is that 4-dimensional space is already known to be a very weird place, where all sorts of surprising things happen. A prime example is the discovery in 1983 of a completely new type of shape in 4-dimensions, one which is completely unsmoothable.
As discussed above, a square is not a smooth shape because of its sharp corners. But it can be smoothed. That is to say, it is topologically identical to a shape which is smooth, namely the circle. In 1983, however, Simon Donaldson discovered a new class of 4-dimensional manifolds which are unsmoothable: they are so full of essential kinks and sharp edges that there is no way of ironing them all out.
Beyond this, it is not only spheres which come in exotic versions. It is now known that 4-dimensional space itself (or R4) comes in a variety of flavours. There is the usual flat space, but alongside it are the exotic R4s. Each of these is topologically identical to ordinary space, but not differentially so. Amazingly, as Clifford Taubes showed in 1987, there are actually infinitely many of these alternative realities. In this respect, the fourth dimension really is an infinitely stranger place than every other domain: for all other dimensions n, there is only ever one version of Rn. Perhaps after all, the fourth dimension is the right mathematical setting for the weird worlds of science fiction writers' imaginations.
About the author
Richard Elwes is a Visiting Fellow at the University of Leeds. He was the winner of the Plus New Writers Award 2006 and has since published articles in New Scientist and Daily Telegraph, and regularly talks about maths in public and on the radio. He is the author of the book Maths 1001, reviewed in Plus, and How to build a brain and 34 other really interesting uses of mathematics (March 2011)
No comments:
Post a Comment