Dear Friends,
Click the link to view the images/access the links.
http://plus.maths.org/content/node/5388
Be Well.
DavidHidden dimensions
by Marianne Freiberger
Shing-Tung Yau.That geometry should be relevant to physics is no surprise — after all, space is the arena in which physics happens. What is surprising, though, is the extent to which the geometry of space actually determines physics and just how exotic the geometric structure of our Universe appears to be.
One mathematician who's got first-hand experience of the fascinating interplay between physics and geometry is Shing-Tung Yau. In a new book called The shape of inner space (co-authored by Steve Nadis) Yau describes how the strange geometrical spaces he discovered turned out to be just what theoretical physicists needed in their attempt to build a theory of everything. Plus met up with Yau on his recent visit to London, to find out more.
Curvature and gravity
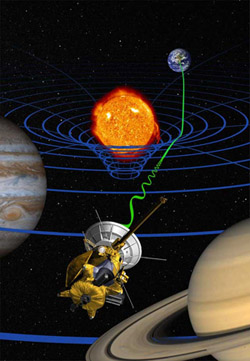An artist's impression of the Sun warping spacetime and the Cassini space probe testing relativity by measuring how signals are delayed by the warping. Image courtesy NASA.An early indication that space is more than just a backdrop for physics came in 1915 when Albert Einstein formed his theory of general relativity. Einstein was working with a four-dimensional spacetime, made up of the three spatial dimensions we're used to and an extra dimension for time. His revolutionary insight was that gravity wasn't some invisible force that propagated through spacetime, but a result of massive bodies distorting the very fabric of spacetime. A famous analogy is that of a bowling ball sitting on a trampoline, which creates a dip that a nearby marble will roll into. According to general relativity, massive objects like stars and planets warp spacetime in a similar way, and thus "attract" other bodies that pass nearby.
Einstein's idea to unify space, time, matter and gravity in this way was completely new — the physicist C.N. Yang has described it as an act of "pure creation". What wasn't new, however, was the mathematics Einstein used to describe the curvature of spacetime. This had been around since the 19th century, when the mathematician Carl Friedrich Gauss and after him his brilliant student Bernhard Riemann had come up with ways of measuring the curvature of an object from the "inside": they no longer needed to refer to a larger space the object might be sitting in. This intrinsic concept of curvature was just what Einstein needed.
"[At the time of Riemann] no-one believed that his new geometry would be useful," explains Yau. "But it turned out that it exactly suited Einstein's purpose. Without Riemann, Einstein would have taken much longer to develop general relativity. This then became an important reason for people to study geometry: geometry motivates physics and physics motivates geometry."
Gravity in a vacuum?
When Yau first learned about general relativity he realised that it posed an interesting theoretical question: could there be a spacetime which contains no matter, a vacuum, in which there still is gravity? The spacetime we live in is not the only one that's possible in terms of general relativity. Einstein's field equations, which describe relativity, also permit other solutions, for example a spacetime without matter and without gravity, in which nothing happens at all. The question was whether a vacuum spacetime which still had some curvature and therefore gravity, was also possible. "In such a spacetime, gravity would be there because of the topology [the shape of the space], rather than because of matter," explains Yau.
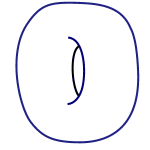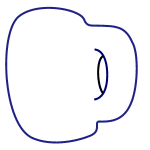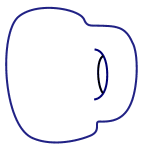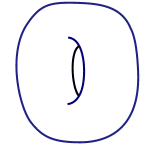A doughnut mug Yau later realised that a geometric version of this question had been asked by the mathematician Eugenio Calabi in the 1950s. Calabi was interested in the interplay between the geometry of an object, that is precise features including size, angles etc, and its topology. Topology is blind to exact measurements and only captures the overall form of an object. A sphere and a deflated football, for example, are very different geometrically, but they are topologically the same because one can be transformed into the other without any tearing or cutting. Similarly, topology regards a doughnut and a coffee cup as equivalent, because one can be morphed into the other. What differentiates the doughnut from a sphere is the fact that it has a hole.
An object with a given topology can be morphed into many different geometric shapes: a sphere into a deflated football, a pyramid, or a cube, etc. Calabi asked himself whether a shape with a certain kind of topology would admit a certain kind of geometry. And it turned out that if the answer was "yes", then the resulting object could be interpreted — in a general relativity setting — as a vacuum in which there was gravity.
Calabi's question
There's no end to the variety of topological shapes you could think of, but topologists usually restrict their attention to what are called manifolds. These are objects that when viewed from up close, look like the ordinary "flat" space (called Euclidean space) we are used to. Spheres and doughnuts, for example, locally look like the flat 2D plane. If you're small enough, you won't notice their curvature, or whether there's a hole in them. You can easily draw a map of a patch of the sphere or doughnut on a flat piece of paper. So these are both 2D manifolds, also called surfaces.
The sphere is a 2D manifold because locally it looks like the Euclidean plane. However, the sphere's curvature means that angles of triangles add up to more than 180 degrees. Image: Lars H. Rohwedder.Another thing the sphere and doughnut have in common is that they're compact: you'd only need a finite number of 2D maps to cover them. This means that they are finite in extent. Given a doughnut or sphere, you can always find a box to fit it into, even if it has to be a very big box.
But manifolds don't have to be two-dimensional. There are also 3D manifolds, which viewed from close up look like the familiar 3D Euclidean space given by three perpendicular coordinate axes. And since it's mathematically possible to think of Euclidean space in any dimension you like (just use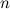 
coordinates rather than just three), there are manifolds of any dimension, too.
coordinates rather than just three), there are manifolds of any dimension, too. Calabi wanted to know what kind of geometry certain compact manifolds could exhibit, in particular, he was interested in curvature. Once you've given a topological manifold (say a sphere) a particular geometric structure (a deflated football), you can measure the curvature of the manifold at every point. This isn't entirely straight-forward: an ant walking around on a saddle will feel upward curvature when it walks up the length of the saddle and downward curvature when it walks down the sides. In this example of a 2D manifold (which is what we consider the saddle to be), you can associate a notion of curvature to various 1D curves passing through a given point.
An ant walking around on a saddle will feel different curvature depending on its path. Image: Eric Gaba. Similarly, in higher dimensions you can associate a notion of curvature to certain 2D surfaces that sit within the larger manifold and contain your point. Taking the average of all the curvatures associated to these 2D surfaces gives what's called the Ricci curvature at the point you're looking at. Since it's an average, Ricci curvature only captures one component of the full notion of curvature as defined by Riemann. This means that a manifold can have zero Ricci curvature at every point without being flat (or having zero Riemannian curvature) overall. In terms of physics, the component captured by Ricci curvature happens to be just the one that describes the curvature of spacetime that's induced by matter being present. So a space with zero Ricci curvature corresponds to a space with no matter — a vacuum in other words.
But Calabi was interested in Ricci curvature for purely geometrical reasons. The mathematician Shiing-shen Chern had shown in the 1940s that a manifold whose Ricci curvature is zero at every point can only have a certain kind of topology. In two dimensions, this corresponds to the rather boring topology of a doughnut. In higher dimensions the topology implied by zero Ricci curvature is a little harder to describe. Mathematicians say that manifolds which have that topology have a vanishing first Chern class.
Calabi turned Chern's question on its head: if you've got a compact manifold with a vanishing first Chern class, can you morph it into a geometric shape which has zero Ricci curvature at every point? Basically, what Calabi was asking is whether a certain type of topology guarantees that a certain type of geometry is possible. However, Calabi was not looking at any old manifold, but restricted his attention to so-called Kähler manifolds. These are easier to deal with because they deviate from Euclidean space in a limited way. They are also what's called complex manifolds: the maps that chart them preserve angles and the manifolds display a certain local symmetry. (The term complex refers to the fact that locally the manifolds look similar not just to plain old Euclidean space, but to something called complex space. In two dimensions this is just the complex plane you might be familiar with if you've studied complex numbers.) Being Kähler makes a manifold accessible to powerful mathematical machinery and also endows it with a special kind of symmetry.
Yau's answer
When Yau first started working on this question in the early 1970s he was primarily motivated by geometry, though, as he tells us, "it was always at the back of my mind that this would be interesting for physics: the construction of a closed universe [the compact manifold] that has no matter [since Ricci curvature is zero] but still has gravity [because of the curvature due to its topology]. But the existence of such a structure would also mean a lot to geometry: Calabi's conjecture provided the clearest way to understand Ricci curvature."
At first Yau, like most other experts, believed that the answer to Calabi's question was "no". Since topology is a much looser concept than geometry, it seemed too much to expect that topology alone could guarantee such a special type of geometry. "For many years I tried to prove that the kind of manifold Calabi was after doesn't exist," he says. "But whatever I tried, I encountered difficulties. So I decided that nature cannot fool me so badly and that there must be something wrong with my reasoning."
In 1977 Yau finally proved that Calabi had been right. To state his result in its full glory, he proved that any compact Kähler manifold with a vanishing first Chern class could be endowed with a geometry with zero Ricci curvature. The kind of manifolds that fit this bill, and they exist in all dimensions, have since become known as Calabi-Yau manifolds.
Hiding dimensions
In 1982 Yau received the Fields medal, the highest honour in mathematics, for his resolution of Calabi's conjecture, which has had a major impact on geometry, as well as for other work. What he didn't know until a little later was that Calabi-Yau manifolds were just what some physicists were looking for. "I was in San Diego with my wife one day [in 1984], looking out at the beautiful ocean," he recalls. "The phone rang and it was my friends Andrew Strominger and Gary Horowitz. They were excited because string theorists were building up models of the Universe and needed to know whether [Calabi-Yau] manifolds really existed. I was happy to confirm that they did."
String theory is an attempt at a "theory of everything" which can explain all the physics in the Universe. Such a theory was, and still is, the holy grail of physics because the two major theories in existence, general relativity (which describes the macroscopic world) and quantum field theory (which describes the world at the sub-atomic scale) contradict each other. String theory resolves the mathematical contradictions by proclaiming that the smallest pieces of matter and energy aren't point-like particles, but tiny little strings. These strings can vibrate, just as guitar strings can vibrate, and the different types of vibration correspond to the fundamental particles and the physical forces we observe.
In the early 1980s string theory was in its infancy. One of its problems was that it needed ten dimensions to work in. Particles and forces were supposed to come from all the different ways in which the strings can vibrate. With less than ten dimensions there simply wouldn't be enough modes of vibration, not enough directions for a string to wriggle in, to produce all the physics we observe. With more than ten dimensions, on the other hand, string theory produced non-sensical predictions. So exactly ten dimensions it had to be. But then how come we can only perceive four of them, three for space and one for time?
Another cross-section of a Calabi-Yau manifold. String theory claims that every point in spacetime is actually a tiny 6D world with the structure of a Calabi-Yau manifold.String theory's answer to this riddle is that the six extra dimensions are rolled up tightly in tiny little spaces too small for us to perceive. "At each point of the 4D spacetime we observe there is in fact a tiny six-dimensional space," Yau explains. These tiny worlds that live at every single point in 4D spacetime are so small, we just can't see them. And what kind of six-dimensional geometrical structure can harbour this hidden world and also satisfy other requirements of string theory? You've guessed it: it has to be a six-dimensional Calabi-Yau manifold. "[Calabi-Yau manifolds] finally provided a concrete geometrical model for string theory," says Yau.
One reason that makes Calabi-Yau manifolds attractive for string theory is their compactness: the manifolds are extremely small, with a diameter somewhere around 10-30cm. That's more than a quadrillion times smaller than an electron. But there are other reasons too. To be consistent with the understanding of physics at the time, the manifolds harbouring the hidden dimensions had to have zero Ricci curvature. What is more, string theory assumes a special kind of symmetry, called supersymmetry, which makes special demands of the geometry of spacetime. These demands make Calabi-Yau manifolds (with their special Kähler symmetry) excellent candidates for string theory, although we still don't know whether they are the only possible solution to the dimensional conundrum.
String future
With the discovery of Calabi-Yau manifolds and other major advances, string theory experienced a landmark year in 1984. But the story didn't end there. A minor blow came in 1986 when it was discovered that string theory needed a slightly amended version of Calabi-Yau manifolds, whose Ricci curvature wasn't zero, but only very nearly zero. What's more, there are many different 6D Calabi-Yau manifolds that could fit the string theory bill and, disappointingly, no-one was able to work out which was the "right" one. All this somewhat undermined the manifolds' standing in physics. However, another boost came when it was discovered that pairs of different Calabi-Yau manifolds can give rise to a theoretical Universe with the same physics. This pairing of manifolds sparked new interest and gave rise to a new notion of symmetry, called mirror symmetry (rather misleadingly, since it's much more complicated that its name suggests).
The precise physical meaning of mirror symmetry is still a mystery, but, as Yau says, it led to "a spectacular new understanding of Calabi-Yau manifolds. It also had lots of rich mathematical consequences that were completely motivated by string theory intuition." In particular, the new notion of mirror symmetry provided a solution to a century-old problem in a nearly forgotten branch of geometry. We won't go into the problem here, but only say that it concerned counting the number of curves that live in particular geometric spaces. Mirror symmetry led to the formula which provided the answer, and its correctness was later proved by Yau and colleagues. (You can find out more about further developments in string theory and Calabi-Yau manifolds in Yau's book.)
Today, string theory is still far from complete. There are many physical quantities it can't yet describe and it has not, and currently cannot, be tested in the lab. Yau, however, believes that its sheer mathematical coherence means that it's not just a red herring. "Mathematicians have been able to prove formulas that were motivated by the physical intuition from string theory. And there are many other spectacular contributions string theory has made to maths. Because of string theory many apparently different areas of maths have merged together in a smooth but totally unexpected manner. This means there must be some truth to string theory. Will it eventually lead to a fundamental theory of matter? It's too early to say, but we believe that there must be some truth to the intuition it provides."
About the author
Marianne Freiberger is co-editor of Plus.
No comments:
Post a Comment